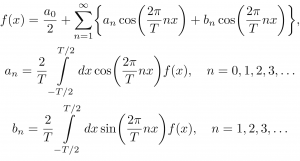実は，有限区間[－T/2, T/2]上で定義された超関数f(x)は三角関数の重ね合わせとして表現できる(フーリエ級数展開)：

診療放射線技師になるための勉強では，特にディジタル画像の取り扱いにおいて，このフーリエ級数展開を多用する．

例えば，前回紹介した階段関数θ(x)を[－π, π]上で定義されたものとしてフーリエ級数展開すると次のようになる：

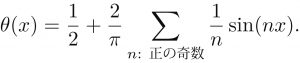
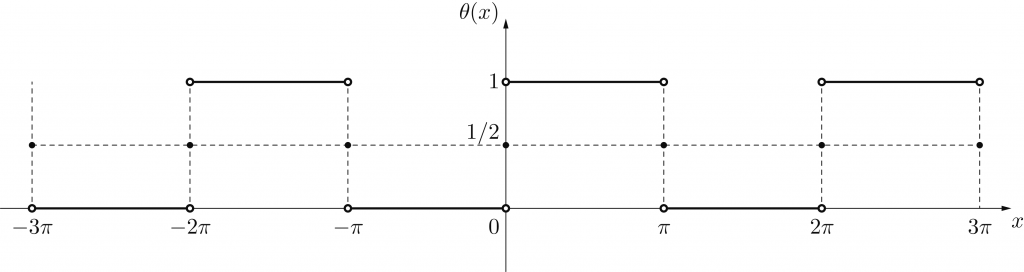
この右辺を真面目に考えると，x = 0において∑の各項は全て0であるため，θ(0) = 1/2であることがわかる．したがって，フーリエ級数展開の式における=は「超関数として等しい」という意味である．超関数であるから，積分に影響が出ない限り1箇所や2箇所の違いがあっても同じ超関数とみなせるのである．

もうひとつ重要な点は，フーリエ級数展開の式を全実数上で定義された超関数とみなすと，[－π, π]上のθ(x)を周期的に拡張したものになるということである．

アイキャッチ画像はフーリエの肖像画．